【分かりやすく解説】投資における複利とは?|『複利は人類最大の発明である』byアインシュタイン

JUN’S カブログへようこそ。
ねぇねぇブタくん!今日もクイズしようか?
ブゥブゥ!(やろうやろう!)
それでは、問題。
「複利は人類最大の発明である」という名言を残したのは誰??
ブゥ!(ウォーレン・バフェットだろ!)
ブゥ!!!
答えは「アインシュタイン」でした!
!!!
じゃあ今日も勉強していこうか笑
投資をしている人なら必ず耳にする
『複利』
これは資産を大きくするには必要不可欠なもの。
先日『72の法則』について記事にしました。
これは「金利の複利効果でお金を2倍にするのに必要な期間を求める法則」でした。
では、ここで出てくる『複利』とは何か。
今日は『複利』について分かりやすく解説します。
複利とは
複利は人類最大の発明である
知ってる人は複利で稼ぎ、知らない人は利息を払う
これは、かの有名なアインシュタインの名言です。
先日これ関してクイズを行ったところ、この名言を残したのはウォーレン・バフェットである。と回答した方が多かったのには驚きました。もちろん間違えですよ。(回答者777名)
有名な学者であるアインシュタインに「複利は人類最大の発明である」と言わしめるほど、「複利」は素晴らしい力を持っています。
また逆に恐ろしい力を持っているのもこの「複利」です。
「複利は~」のくだりは知っている人も多いと思いますが、その続きの「知ってる人は複利で稼ぎ、知らない人は利息を払う」までは知らない人もいたのではないでしょうか。
それでは、複利について実際に見ていきましょう。
金利の計算方法には単利と複利の2種類ある
単利式
元本部分に対してのみ利息がつく
元本は預けた当初の金額から増えない
複利式
元本部分に対してつく利息を次の元本に組み入れる方式
利息を組み入れた元本は当初の金額より増えていく
運用後資産の計算式 n年後の資産
単利式
元本×(1+金利×n)
複利式
元本×(1×金利)^n
※(^n=n乗)
例えば100万円を年利5%で10年間運用したケースで見てみましょう。
単利と複利で計算するとこのような違いになります。
単利の場合
1年目 100万円×1.05%=105万円
2年目 100万円×1.05%+5万円=110万円
3年目 100万円×1.05%+10万円=115万円
・
・
・
10年目 100万円×1.05%+45万円=150万円
(※単利の利息は元本にのみかかります。)
複利の場合
1年目 100万円×1.05%=105万円
2年目 105万円×1.05%=110.25万円
3年目 110.25万円×1.05%=115.7625万円
・
・
・
10年目 155.13万円×1.05%=162.88万円
(※利息は次の元本に組み入れて計算します。)
上記のような運用した場合、複利の方が約13万円も多く増えることになるんです。
凄いですよね?
利率や元本が大きいほど複利の力が偉大なのががわかります。
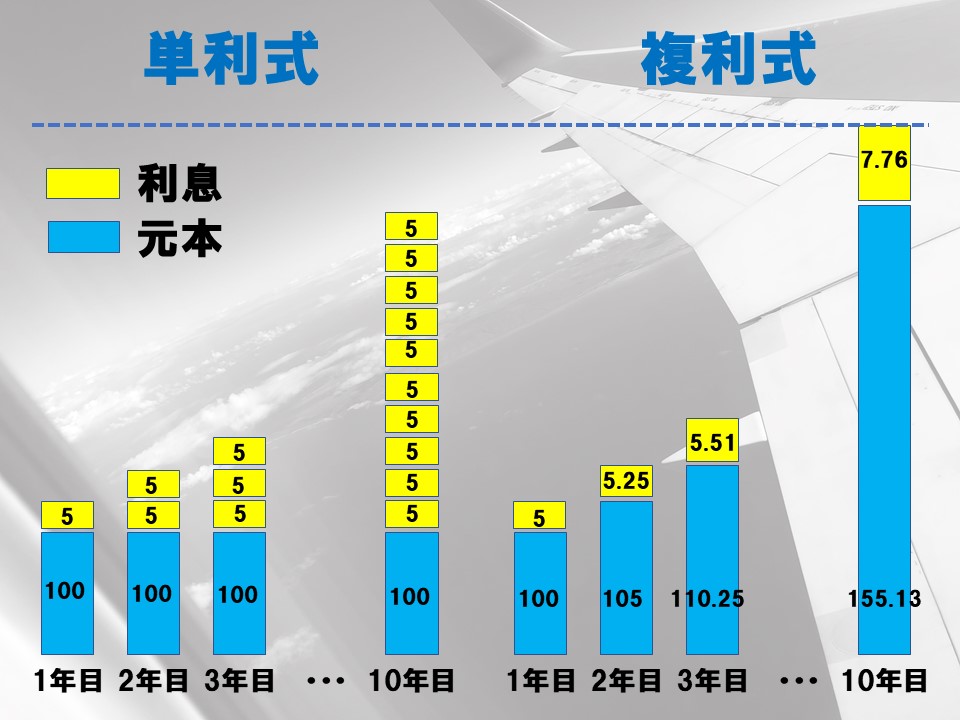
このグラフのようなイメージです。
複利の方は、ついた利息が次の元本に含まれて計算されます。これが大きな違いです。
また、同じ複利でも期間の違いでこんなに大きな差になることにも驚きです。
これは少し極端な例ですが、まさに雪だるま式に資産が増える。そんな力を持っているのが「複利の力」です。
まとめ
金利の計算方法には単利と複利の2種類ある
単利式
元本部分に対してのみ利息がつく
元本は預けた当初の金額から増えない
複利式
元本部分に対してつく利息を次の元本に組み入れる方式
利息を組み入れた元本は当初の金額より増えていく
運用後資産の計算式 n年後の資産
単利式
元本×(1+金利×n)
複利式
元本×(1×金利)^n
※(^n=n乗)
配当金をもらうと嬉しいですが、嬉しいからといってそれを使ってしまってはお金はなかなか増えません。
配当金を再投資することで、はじめは小さな複利効果しか生まれませんが、いずれ大きな配当金を生み出す元本となってくれるのです。
たかが配当金、されど配当金です。
小さな雪だるまがいずれ大きな雪だるまになる日まで少しずつ、ゆっくりと転がしましょう♪
今の説明でもまだよくわからない。実感が湧かないよという方は、実際に自分の資産やこれから投資する予定の投資先の利回りで計算してみてくださいね。
きっと『複利の力』に驚くと思いますよ。
さぁ皆さんも複利の力で稼ぐ人になりましょう♪
JUN
